MA.5.1 积分

#单变量函数微分学 #积分

一、定积分的定义

曲边梯形面积

(1) 分割
用分点 $a = x_{0} < x_{1} < \dots < x_{n} = b$ 将 $[a, b]$ 分为 $n$ 个小区间 $[x_{i - 1}, x_{i}] (i = 1, 2, \dots, n)$ , 其长度记为 $Δ x_{i} = x_{i} - x_{i - 1}$
(2) 作近似和
$\forall ξ_{i} \in [x_{i - 1}, x_{i}]$ ,第 $i$ 个小曲边梯形面积 $Δ S_{i} \approx$ $f (ξ_{i}) Δ x_{i}$ , 故曲边梯形面积

A = \sum_{i = 1}^{n} Δ S_{i} \approx \sum_{i = 1}^{n} f (ξ_{i}) Δ x_{i}

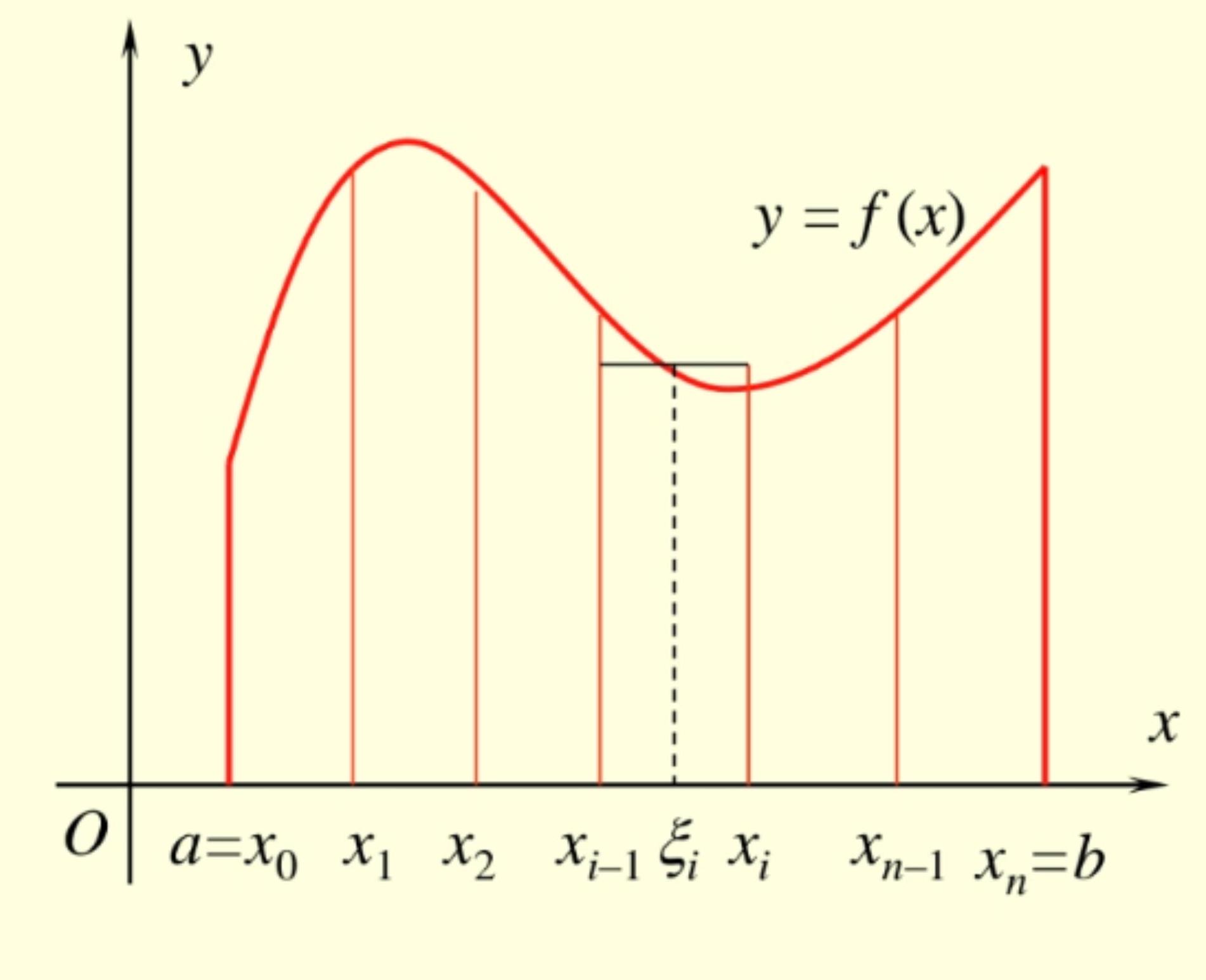
../res/2023_11_30_371e33ffbe2119eb668cg-1.jpg|200

(3) 取极限
记 $∥ T ∥ = max_{1 \leq i \leq n} Δ x_{i}$ , 则曲边梯形面积

A = lim_{∥ T ∥ \to 0} \sum_{i = 1}^{n} f (ξ_{i}) Δ x_{i}

变速直线运动位移

Question

质点以速度 $v = v (t) (\in C [a, b])$ 作直线运动,
如何求 $[a, b]$ 内质点的位移 $s ?$

(1) 分割 用分点 $a = t_{0} < t_{1} < \dots < t_{n} = b$ 将 $[a, b]$ 分为 $n$ 个小区间 $[t_{i - 1}, t_{i}] (i = 1, 2, \dots, n)$ , 其长度记为 $Δ t_{i} = t_{i} - t_{i - 1}$
(2) 作近似和 $\forall ξ_{i} \in [t_{i - 1}, t_{i}]$ , 时段 $[t_{i - 1}, t_{i}]$ 经过路程 $Δ s_{i}$ $\approx v (ξ_{i}) Δ t_{i}$ , 故 $[a, b]$ 内经过路程

s = \sum_{i = 1}^{n} Δ s_{i} \approx \sum_{i = 1}^{n} v (ξ_{i}) Δ t_{i}

(3) 取极限 记 $∥ T ∥ = max_{1 \leq i \leq n} Δ t_{i}$ , 则时间 $[a, b]$ 内路程

s = lim_{∥ T ∥ \to 0} \sum_{i = 1}^{n} v (ξ_{i}) Δ t_{i}

Question

设一个线密度为 $\ln x$ 的木棒，
计算木棒质量?

定积分

#定积分

分割 $T : a = x_{0} < x_{1} < \dots < x_{n} = b$ . 其模 $∥ T ∥ = max_{1 \leq i \leq n} {Δ x_{i}}$

设 $f : [a, b] \to R$ . 任取 $[a, b]$ 分割 $T$ 及 $\forall ξ_{i} \in [x_{i - 1}, x_{i}]$ $({ξ_{1}, ξ_{2}, \dots, ξ_{n}} = ξ (T)$ 称为分割 $T$ 下介点集), 作和

S_{n} (T) = \sum_{i = 1}^{n} f (ξ_{i}) Δ x_{i}

若

lim_{∥ T ∥ \to 0} \sum_{i = 1}^{n} f (ξ_{i}) Δ x_{i} = I \dots (I 与 T, ξ_{i} 均无关)

则称 $f$ 在 $[a, b]$ 上可积, $I$ 称为 $f$ 在 $[a, b]$ 上的定积分, 记为

I = \int_{a}^{b} f (x) d x

$f (ξ_{i}) \to f (x); Δ x_{i} \to d x; lim \sum \to \int$
$\int$ 一积分号; $a, b$ 一积分下、上限; $[a, b]$ 一积分区间;
$f (x)$ 一被积函数; $x$ 一积分变量.

Riemann和或积分和

$\Leftrightarrow$ Riemann 可积，Riemann积分

#Riemann和

$S_{n} (T) = \sum_{i = 1}^{n} f (ξ_{i}) Δ x_{i}$

其极限值 $I$ 为对应 $[a, b]$ 上的定积分

$f \in R [a, b]$ 的含义?

$f \in [a, b]$ 上 Riemann 可积的函数集合

可积与不可积的 “ $ε - δ$ ” 表述 ?

#可积

$f \in R [a, b]$ , 即

$\exists I \in R, \forall ε > 0, \exists δ > 0, \forall ∥ T ∥ < δ, \forall ξ (T)$

| \sum_{i = 1}^{n} f (ξ_{i}) x_{i} \cdot I | < ε

#不可积

$f \notin R [a, b]$ 即

$\forall I \in R, \exists ε > 0, \forall δ > 0, \exists ∥ T ∥ < δ, \exists ξ (T)$

| \sum_{i = 1}^{n} f (ξ_{i}) x_{i} \cdot I | ⩾ ε

定积分值与积分区间和被积函数有关, 与 $[a, b]$ 的分割和介点集无关, 也与积分变量无关, 即$$\int_{\textcolor{orange}a}^{\textcolor{orange}b} \textcolor{orange}f(x) \mathrm{d} x=\int_{a}^{b} f(t) \mathrm{d} t=\int_{a}^{b} f(u) \mathrm{d} u$$
若存在两分割或同一分割下不同介点集, 使积分和的极限不同, 则 $f$ 在 $[a, b]$ 不可积!
- i.e. 不同黎曼和(分割可不同), 但极限不同 $\Rightarrow$ 不可积

例题

例 1

证明Dirichlet函数 $D (x) = {\begin{cases} 1, & x \in Q \\ 0, & 其它 \end{cases}$ 在 $[0, 1]$ 不可积

Tips
(介点集+稠密性)
注意到Dirichlet函数的取值和自变量是否为有理数相关，据此构造不同的介点

Solution
$\forall$ 取 $[0, 1]$ 分割 $T$ ，取 $ξ_{1} \in [x_{i - 1}, x_{i}] \cap Q$ 则
$\sum_{i = 1}^{n} D (ξ_{i}) Δ x_{i} = \sum_{i = 1}^{n} \cdot 1 Δ x_{i} = 1 \overset{∥ T ∥ \to 0}{\to} 1$
再取 $η_{i} \in [x_{i - 1}, x_{i}] \cap Q^{C}$ 则
$\sum_{i = 1}^{n} D (η_{i}) Δ x_{i} = \sum_{i = 1}^{n} 0 \cdot Δ x_{i} = 0 \overset{∥ T ∥ \to 0}{\to} 0$
矛盾

二、可积函数类

可积的必要条件

若 $f \in R [a, b]$ , 则 $f$ 在 $[a, b]$ 有界

有界是可积的必要不充分条件
无界不可积, 可积必有界
有界 $⇏$ 可积: Dirichlet函数

Tips
先由条件入手，橙色字体由逆推之后获得

Proof
反证

若 $f$ 在 $[a, b]$ 无界:
$\forall I \in R,$ 取 $ε = 1$ , $\forall δ > 0$ , 取 $∥ T ∥ < δ$

由于 $f$ 在 $[a . b]$ 无界
故 $f$ 在该分割下至少一个子区间无界

不妨为第 $n$ 个区间: $[x_{n - 1}, x_{n}]$ :
取 $ξ_{i} = x_{i} (1 \leq i \leq n - 1)$ , $ξ_{n} \in [x_{n - 1}, x_{n}]$ 满足
$| f (ξ_{n}) | > \frac{1 + | \sum_{i = 1}^{n - 1} f (ξ_{i}) - I |}{Δ x_{n}}$ $\begin{aligned} | \sum_{i = 1}^{n} f (ξ_{i}) Δ x_{i} - I | & = | f (ξ_{n}) Δ x_{n} + \sum_{i = 1}^{n - 1} f (ξ_{i}) Δ x_{i} - I | \\ ⩾ | f (ξ_{n}) | Δ x_{n} - | \sum_{i = 1}^{n - n} f (ξ_{i}) Δ α_{i} \cdot I | \\ ⩾ ε \dots 取 ε_{0} = 1 \end{aligned}$
故 $f \notin R [a, b]$

常见的可积条件==（闭区间）==

闭区间连续必可积

若 $f \in C [a, b]$ , 则 $f \in R [a, b]$ .

闭区间有限间断+有界可积

若 $f$ 在 $[a, b]$ 有界, 且仅有限个间断点, 则 $f \in R [a, b]$

无限个间断 $⇏$ 不可积(是否为可数无限)

闭区间单调可积

若 $f$ 在 $[a, b]$ 单调, 则 $f \in R [a, b]$

例题

例2

函数 $f (x) = {\begin{array}{cc} \frac{1}{n}, & \frac{1}{n + 1} < x \leq \frac{1}{n}, (n = 1, 2, \dots) \\ 0, & x = 0 \end{array}$ 在 $[0, 1]$ 可积

Analysis
画图可知间断点全为跳跃间断点： $0; \frac{1}{2} \cdot \frac{1}{3} \dots \frac{1}{n}$

单增=>可积

三、积分例子初识

例题

例3

$\int_{a}^{b} c d x = c (b - a)$

例4

证明 $\int_{a}^{b} x^{2} d x = \frac{1}{3} (b^{3} - a^{3})$

Tips
取特殊的分割/介点集

Proof
将 $[a, b]$ $n$ 等分
$x_{k} = a + k h$ , 其中 $h = \frac{b - a}{n}$

取 $ξ_{k} = x_{k}$ (右端点)
则
$\begin{aligned} \sum_{k = 1}^{n} x_{k}^{2} \cdot h & = \sum_{k = 1}^{n} (a + k h)^{2} h \\ = h \sum_{k = 1}^{n} (a^{2} + 2 a k h + k^{2} h^{2}) \\ = n a^{2} h + 2 a h^{2} \cdot \frac{n (n + 1)}{2} + h^{3} \frac{n (n + 1) (2 n + 1)}{6} \\ = a^{2} (b - a) + a \cdot \frac{n (n + 1)}{n^{2}} (b - a)^{2} + \frac{(n + 1) (2 n + 1)}{6 n^{3}} (b - a)^{3} \\ \overset{n \to \infty}{\to} a^{2} (b - a) + a (b - a)^{2} + \frac{1}{3} (b - a)^{3} \\ = \frac{1}{3} (b^{3} - a^{3}) \end{aligned}$
故 $\int_{a}^{b} x^{2} d x = \frac{1}{3} (b^{3} - a^{3})$

例5

$★$ 设 $c \in [a, b] . J (x) = {\begin{array}{lc} 0, & x \in [a, b] ∖ {c}, \\ 1, & x = c . \end{array}$ 证明

\int_{a}^{b} J (x) d x = 0

Proof
$\begin{aligned} \forall T \forall ξ (T) \\ 0 \leq \sum_{i = 1}^{n} J (ξ_{i}) Δ x_{i} \leq 2 ∥ T ∥ \to 0 \\ c可能在分界点中: 至多两项 \\ 故: \int_{a}^{b} J (x) d x = 0 \end{aligned}$

Corollary

$J (x)$ 有限个点值不为0，结论不变

四、积分的基本性质

Tip

规定

\int_{a}^{b} f (x) d x = - \int_{b}^{a} f (x) d x, \int_{a}^{a} f (x) d x = 0

Analysis
$\overset{a x_{i - 1} x_{i} b}{\to}$ = $\overset{b x_{i} x_{i - 1} a}{\to}$
$\begin{aligned} \int_{a}^{b} f (x) d x = lim_{∥ T ∥ \to 1} \sum_{i = 1}^{n} f (ξ_{i}) (x_{i} - x_{i - 1}) \\ \int_{b}^{a} f (x) d x = lim_{∥ T ∥ \to 0} \sum_{i = 1}^{n} f (ξ_{i}) (x_{i - 1} - x_{i}) \end{aligned}$

可加性

#积分/可加性

设 $f \in R [a, b]$ , 则 $f$ 在 $[a, c]$ 和 $[c, b]$ 可积, 且

\int_{a}^{b} f (x) d x = \int_{a}^{c} f (x) d x + \int_{c}^{b} f (x) d x .

且
$\begin{aligned} \int_{a}^{c} f (x) d x & = \int_{a}^{b} f (x) d x - \int_{c}^{b} f (x) d x \\ = \int_{a}^{b} f (x) d x + \int_{b}^{c} f (x) d x \end{aligned}$
$\Rightarrow$ 无需限定 $c$ 在 $[a, b]$ 内

※子区间可积

Corollary

若 $f \in R [a, b]$ , 则对 $[α, β] \subset [a, b]$ 有 $f \in R [α, β]$

线性性

#积分/线性性

若 $f, g \in R [a, b]$ , 则 $α f \pm β g \in R [a, b]$ , 且

\int_{a}^{b} [α f (x) \pm β g (x)] d x = α \int_{a}^{b} f (x) d x \pm β \int_{a}^{b} g (x) d x

$\Rightarrow$ 改变有限点不改变可积性一S积分值

数乘、加法线性组合

※改变有限点不改变可积性与积分值

Corollary

设 $f \in R [a, b]$ , 除有限点外 $g (x) = f (x)$ . 有

g \in R [a, b] 且 \int_{a}^{b} g (x) d x = \int_{a}^{b} f (x) d x

$g$ 相当于 $f$ 修改有限个点得到
改变有限点不改变可积性与积分值
不可积若可以，则改回去（矛盾）
应用: 可知 $\int_{a}^{b} \frac{\sin x}{x} d x$ 存在, 由于可补充定义 $x = 0$ 时

Proof

令 $J (x) := g (x) - f (x)$ 则
$J (x)$ 除有限点外均为 $0$
故 $J \in R [a, b]$ 且 $\int_{a}^{b} J (x) d x = 0$

又 $g (x) = f (x) + J (x)$
故 $g \in R [a, b]$ 且 $\int_{a}^{b} g (x) d x = \int_{a}^{b} f (x) d x + \int_{a}^{b} J (x) d x = \int_{a}^{b} f (x) d x$

保号性

#积分/保号性

若 $f \in R [a, b]$ , 且 $f (x) \geq 0$ , 则 $\int_{a}^{b} f (x) d x \geq 0$

Tips
出现 $[a, b]$ ，默认 $a ⩽ b$

根据保号性可推出以下推论:

单调性

#积分/单调性

若 $f, g \in R [a, b]$ , 且 $f (x) \leq g (x)$ , 则

\int_{a}^{b} f (x) d x \leq \int_{a}^{b} g (x) d x

Proof
$\begin{aligned} 令 & F (x) = g (x) - f (x) ⩾ 0 . 且FeR[a,b] \\ 故 & \int_{a}^{b} F (x) = \int_{a}^{b} g (x) - \int_{a}^{b} f (x) ⩾ 0 \\ ∴ & \int_{a}^{b} f (x) d x \leq \int_{a}^{b} g (x) d x \end{aligned}$

估值性

#积分/估值性

若 $f \in R [a, b]$ , 且 $m \leq f (x) \leq M$ , 则

m (b - a) \leq \int_{a}^{b} f (x) d x \leq M (b - a)

Analysis
取 $g (x) = M or m$ 即可

※积分绝对值不超过绝对值的积分

#积分/绝对值积分绝对值不超过绝对值的积分

若 $f \in R [a, b]$ , 则 $| f | \in R [a, b]$ , 且

| \int_{a}^{b} f (x) d x | \leq \int_{a}^{b} | f (x) | d x

Proof
即证: $$-\int_{a}^{b}|f(x)| d x \leqslant \int_{a}^{b} f(x) d x \leq \int_{a}^{b}|f(x)| d x$$

由于 $\forall α \in [a, b], - | f (x) | \leq f (x) \leq | f (x) |$

由 #积分/估值性三边积分:
$- \int_{a}^{b} | f (x) | d x ⩽ \int_{a}^{b} f (x) d x ⩽ \int_{a}^{b} | f (x) | d x$

../res/2023_11_30_371e33ffbe2119eb668cg-5.jpg|300

Question

由 $| f | \in R [a, b]$ 能否导出 $f \in R [a, b]$ ?

不能

Analysis
运用Drichlet函数即可

反例如下:
$\begin{aligned} f (x) = D (x) - \frac{1}{2} = {\begin{cases} \frac{1}{2} & , D \in Q \\ - \frac{1}{2} & , D \in Q^{c} \end{cases} \\ D (x) \notin R [a, b] \\ \Rightarrow f (x) \notin R [a, b] \\ 但 | f (x) | = \frac{1}{2} \end{aligned}$

🔴积分中值定理

#积分/中值定理

设 $f \in C [a, b]$ , 则 $\exists ξ \in [a, b]$ 使得

\int_{a}^{b} f (x) d x = f (ξ) (b - a)

几何意义 “化曲为方”
$f$ 在 $[a, b]$ 的平均值:
$\frac{1}{b - a} \int_{a}^{b} f (x) d x$

Proof

设 $f$ 在 $[a, b]$ 上最大小值为M， m，则:
$\forall x \in [a, b], m ⩽ f (x) ⩽ M$
由 #积分/估值性
$\begin{aligned} M (b - a) & \leq \int_{a}^{b} f (x) d x \leq M (b - a) . \\ ∴ M & = \frac{\int_{a}^{b} f (x) d x}{b - a} \leq M \end{aligned}$
由 #闭区间连续函数介值性 :
$\exists {\in [a, b], 使 \frac{\int_{a}^{b} f (x) d x}{b - a} = f (ξ)$
平均值为: $\frac{1}{n} \sum_{i = 1}^{n} f (ξ_{i}) = \frac{1}{b - a} \sum_{i = 1}^{n} f (ξ_{i}) \underset{Δ x_{i}}{\underset{⏟}{\frac{b - a}{n}}} \overset{n \to \infty}{\to} \frac{1}{b - a} \int_{a}^{b} f (x) d x$

#积分/中值定理/推广

$\int_{a}^{b} f (x) g (x) d x = f (ξ) \int_{a}^{b} g (x) d x, ξ \in [a, b]$

Proof
见作业

五、微积分基本定理

变上限积分

若 $f \in R [a, b]$ , 称

φ (x) = \int_{a}^{x} f (t) d t, x \in [a, b]

为 $f$ 在 $[a, b]$ 上的变上限积分

连续性

#积分/连续性

若 $f \in R [a, b]$ , 则 $φ (x) \in C [a, b]$

Proof

$\forall α \in [a, b]$ 给 $Δ x \neq 0$ , 则
$\begin{aligned} Δ φ & = φ (x + Δ x) - φ (x) \\ = \int_{a}^{x + Δ x} f (t) d t - \int_{a}^{x} f (t) d t \\ = \int_{x}^{α + Δ x} f (t) d t \end{aligned}$ $\begin{aligned} \Rightarrow | Δ φ | & = | \int_{x}^{x + Δ x} f (t) d t | \leq | \int_{x}^{x + Δ x} | f (t) | d t | \\ \leq μ | σ x | \\ \overset{Δ x \to 0}{\to} 0 \end{aligned}$
$即 φ 在 x 处连续$

可导性

#积分/可导性

若 $f$ 在 $x_{0}$ 连续, 则 $φ$ 在 $x_{0}$ 可导, 且

φ^{'} (x_{0}) = f (x_{0})

Analysis

即证: $lim_{x \to x_{0}} \frac{φ (x) - φ (x_{0})}{x - x_{0}} = f (x_{0})$

考虑: $\frac{φ (x) - φ (x_{0})}{x - x_{0}} - f (x_{0}) : \frac{\int_{a}^{x} f (t) d t - \int_{0}^{x_{0}} f (t) d t}{x - x_{0}}$
$\begin{aligned} \frac{φ (x) - φ (x_{0})}{x - x_{0}} - f (x_{0}) \\ = & \frac{\int_{a}^{x} f (t) d t - \int_{a}^{x_{0}} f (t) d t}{x - x_{0}} - f (x_{0}) \\ = & \frac{\int_{x_{0}}^{x} f (t) d t - (x - x_{0}) f (x_{0})}{x - x_{0}} \\ = & \frac{\int_{x_{0}}^{x} f (t) d t - \int_{x_{0}}^{x} f (x_{0}) d t}{x - x_{0}} \\ = & \frac{\int_{x_{0}}^{x} [f (t) - f (x_{0})] d t}{x - x_{0}} \end{aligned}$
$x \to x_{0}, t \in [x_{0}, x] ⟹ t \to x_{0}$

$⟹ | [◻] | < ε$

Proof

由 $f$ 在 $x_{0}$ 连续:

即: $lim_{t \to x_{0}} f (t) = f (x_{0})$

故: $\forall ε > 0, \exists δ > 0$ ，使 $\forall | t - x_{0} | < δ$ .

$| f (t) - f (x_{0}) | < ε$

从而 $\forall 0 < | x - x_{0} | < δ$ 时, 有
$\begin{aligned} | \frac{φ (x) - φ (x_{0})}{x - x_{0}} - f (x_{0}) | \\ = \frac{| \int_{x_{0}}^{x} [f (t) - f (x_{0})] d t |}{| x - x_{0} |} \\ \leq \frac{| \int_{x_{0}}^{x} | f (t) - f (x_{0}) | d t |}{| x - x_{0} |} \\ \leq \frac{ε | x - x_{0} |}{| x - x_{0} |} \\ = ε \end{aligned}$

#定积分的导数

若 $f \in C [a, b]$ , 则 $φ (x) \in D [a, b]$ , 且

φ^{'} (x) = \frac{d}{d x} \int_{a}^{x} f (t) d t = f (x)

例题

变上限积分求导

=

被积函数上限处值

\times

上限求导

Example

例6 求下列导数

$\frac{d}{d x} \int_{a}^{x} t \cos t d t$

$= x \cdot \cos x$

Example

2) $\frac{d}{d x} \int_{a}^{x} x \cos t d t$

$x$ 为给定的:
$\begin{aligned} 原式 & = \frac{d}{d x} x \int_{a}^{x} \cos t d t \\ = \int_{a}^{x} \cos t d t + x \frac{d}{d x} \int_{a}^{x} \cos t d t \\ = \int_{a}^{x} \cos t d t + x \cdot \cos x \end{aligned}$

Example

3) $\frac{d}{d x} \int_{0}^{\sqrt{x}} \sin t^{2} d t$

令 $\sqrt{x} = u$

$φ (u) = \int_{0}^{u} \sin t^{2} d t \Rightarrow$ 所给 $φ (\sqrt{x})$
$\begin{aligned} 原式 & = \frac{d}{d x} φ (\sqrt{x}) \\ = φ^{'} (u) (\sqrt{x})^{'} \\ = \sin u^{2} \cdot \frac{1}{2 \sqrt{x}} \\ = \frac{\sin x}{2 \sqrt{x}} \end{aligned}$

变上限积分求极限

Example

例7 求极限 $lim_{x \to 0^{+}} \frac{\int_{0}^{x^{2}} \sin \sqrt{t} d t}{x^{3}}$

用洛必达 $\frac{0}{0}$ , 不用等价无穷小
$\begin{aligned} 原式 & \overset{\frac{0}{0}}{=} lim_{x \to 0} \frac{\sin \sqrt{x^{2}} 2 x}{3 x^{2}} \\ = lim_{x \to 0} \frac{2 \sin x}{3 x} \\ = \frac{2}{3} \end{aligned}$

Example

P191.18.(2) $lim_{x \to 0} \frac{1}{\sin^{3} x} \int_{0}^{\tan x} \arcsin t^{2} d t$

Solution
$\begin{aligned} \overset{\frac{0}{0}}{=} lim_{x \to 0} \frac{\arcsin (\tan x)^{2}}{3 \sin^{2} x \cos x \cos^{2} x} \\ = lim_{x \to 0} \frac{\arcsin^{2} x}{3 x^{2} \cos x^{3}} \\ = lim_{x \to 0} \frac{x^{2}}{3 x^{2}} \\ = \frac{1}{3} \end{aligned}$

Example

P191.18.(4) $lim_{n \to \infty} \frac{1^{p} + 2^{p} + \dots + n^{p}}{n^{p + 1}}$

Solution
$\begin{aligned} = lim_{n \to \infty} \frac{\int_{1}^{n} t^{p} d t}{n^{p + 1}} \\ = lim_{n \to \infty} \frac{n^{p}}{(p + 1) n^{p}} \\ = \frac{1}{p + 1} \end{aligned}$

借助 #积分/中值定理求变上限积分的极限

Example

P191.19.(2) $lim_{n \to \infty} \int_{0}^{1} \frac{x^{n}}{1 + x} d x$

Solution

由 #积分/中值定理/推广

$\int_{0}^{1} \frac{x^{n}}{1 + x} d x = \frac{\int_{0}^{1} x^{n} d x}{1 + ξ},$ $ξ \in [0, 1]$
$\begin{aligned} 即 \\ \begin{aligned} 原式 & = \frac{1}{1 + ξ} \cdot lim_{n \to \infty} \int_{0}^{1} x^{n} d x \\ = \frac{1}{1 + ξ} \cdot lim_{n \to \infty} (\frac{1}{n + 1} x^{n + 1} |_{0}^{1}) \\ = \frac{1}{1 + ξ} \cdot lim_{n \to \infty} \frac{1}{n + 1} & \frac{1}{1 + ξ} 有界 \\ = 0 \end{aligned} \end{aligned}$

Example

P191.19.(3) $lim_{n \to \infty} \int_{n}^{n + a} \frac{\sin x}{x} d x$

Solution

由 #积分/中值定理
$\begin{aligned} lim_{n \to \infty} \int_{n}^{n + a} \frac{\sin x}{x} d x = lim_{n \to \infty} \frac{\sin ξ}{ξ}, ξ \in [n, n + a] \\ ∴ n \to \infty 时 ξ \to \infty \\ \begin{aligned} 故原式 & = lim_{ξ \to \infty} \frac{\sin ξ}{ξ} \\ = 0 \end{aligned} \end{aligned}$

原函数存在定理

#原函数存在定理

若 $f \in C [a, b]$ , 则 $f$ 存在原函数 $F (x)$ , 且

F (x) = \int_{a}^{x} f (t) d t + C

微积分基本定理

#微积分基本定理

设 $f \in C [a, b]$ , 且 $F^{'} (x) = f (x)$ , 则

\int_{a}^{b} f (x) d x = {F (x) |}_{a}^{b} = F (b) - F (a)

Proof

由于连续，知: $F (x) = \int_{a}^{x} f (t) d t + c$ . 令 $x = a$

设: $c : F (a)$ ，从而 $\int_{a}^{x} f (t) d t = F (x) - C = F (x) - F (a)$

$\overset{令 x = b}{\to} \int_{a}^{b} f (t) d t = F (b) - F (a)$

🔴弱形式 N-L公式

#N-L公式

设 $f \in R [a, b], F \in C [a, b]$ 且 $F^{'} (x) = f (x), x \in (a, b)$ 则

\int_{a}^{b} f (t) d t = F (b) - F (a)

（弱化在： $f$ 可积不一定连续）

Analysis

运用定义：Riemann和取极限

Proof
$\begin{aligned} \forall 取分割T: a = x_{0} < x_{1} < \dots < x_{n} = b \\ 差分得: \\ F (b) - F (a) = F (x_{n}) - F (x_{0}) = \sum_{i = 1}^{n} [F (a_{i}) - F (a_{i - 1})] \\ 由Lagrange \\ \overset{\exists ξ_{i} \in (x_{i + 1}, x_{i})}{=} \sum_{i = 1}^{n} F^{'} (ξ_{i}) Δ x_{i} \\ = \sum_{i = 1}^{n} f (ξ_{i}) Δ x_{i} \\ \Rightarrow F (b) - F (a) = lim_{| | T | | \to 0} \sum_{i = 1}^{n} f (ξ_{i}) Δ x_{i} = \int_{a}^{b} f (x) d x \end{aligned}$

Example

Eg. $\int_{a}^{b} x^{2} d x = {\frac{x^{3}}{3} |}_{a}^{b}$

Solution

$= \frac{1}{3} (b^{3} - a^{3})$

Example

例8 计算 $\int_{0}^{2 π} | \sin x | d x$

Solution
$\begin{aligned} \int_{0}^{2 π} | \sin x | d x \\ = \int_{0}^{π} \sin x d x - \int_{π}^{2 π} \sin x d x \\ = - {\cos x |}_{0}^{π} + {\cos x |}_{π}^{2 π} \\ = 2 + 2 \\ = 4 \end{aligned}$

Example

例9 计算 $\int_{- 1}^{1} sgn x d x$

Analysis
$\begin{aligned} 有第一类间断点 \Rightarrow 无导数 \Rightarrow 无原正数 \\ \Rightarrow 分段 \end{aligned}$
Proof
$\begin{aligned} 原式 & = \int_{- 1}^{0} sgn x d x + \int_{0}^{1} sgn x d x \\ = \int_{- 1}^{0} - 1 d x + \int_{0}^{1} 1 d x & \dots 改变有限点，不改变积分值 \\ = - 1 + 1 \\ = 0 \end{aligned}$

Example

例10 计算 $\int_{0}^{1} \frac{x^{2} + 1}{x^{4} + 1} d x$

Solution
$\begin{aligned} = \int_{0}^{1} \frac{1 + \frac{1}{x^{2}}}{x^{2} + \frac{1}{x^{2}}} d x \\ = \int_{0}^{1} \frac{d (x - \frac{1}{x})}{{(x - \frac{1}{x})}^{2} + (\sqrt{2})^{2}} \\ = {\frac{1}{\sqrt{2}} \arctan \frac{x - \frac{1}{x}}{\sqrt{2}} |}_{0}^{1} + c \end{aligned}$
$0$ 处无意义: 补充极限

令 $F (x) = {\begin{cases} \frac{1}{\sqrt{2}} \arctan \frac{x - \frac{1}{x}}{\sqrt{2}}, 0 < x \leq 1 \\ - \frac{1}{\sqrt{2}} \frac{π}{2} x = 0 \end{cases}$

则 $F (x) \in C [0, 1] \cap D (0.1)$

且 $F^{'} (x) = \frac{x^{2} + 1}{x^{4} + 1}, x \in (0, 1]$
$\begin{aligned} ∴ 原积分 & = {F (x) |}_{0}^{1} + C \\ = \frac{π}{2 \sqrt{2}} \end{aligned}$

Example

$\int_{0}^{π} \frac{d x}{1 + \cos^{2} x}$

Wrong Solution
$\begin{aligned} = \int_{0}^{π} \frac{\frac{1}{\cos^{2} x} d x}{\frac{1}{\cos^{2} x} + 1} \\ = \int_{0}^{π} \frac{d \tan x}{2 + \tan^{2} x} \\ \neq {\frac{1}{\sqrt{2}} \arctan \frac{\tan x}{\sqrt{2}} |}_{0}^{π} = 0 \end{aligned}$
该函数在 $x = \frac{π}{2}$ 无意义

不是原函数=>分段

Correct Solution
$\begin{aligned} = \int_{0}^{π / 2} \frac{d \tan x}{2 + \tan^{2} x} + \int_{\frac{π}{2}}^{π} \frac{d \tan x}{2 + \tan^{2} x} \\ = \frac{1}{\sqrt{2}} \arctan \frac{\tan x}{\sqrt{2}} |_{0}^{π / 2} + \frac{1}{\sqrt{2}} \arctan \frac{\tan x}{\sqrt{2}} |_{\frac{π}{2}}^{π} \\ = \frac{1}{\sqrt{2}} (\frac{π}{2} - 0) + \frac{1}{\sqrt{2}} [0 - (- \frac{π}{2})] \\ = \frac{π}{\sqrt{2}} \end{aligned}$

六、定积分的计算

换元积分法

#换元积分法

设 $f \in C [a, b], x = φ (t) \in C^{(1)} [α, β] (或 [β, α]),$ 且 $φ (α) = a, φ (β) = b, 则,$

\int_{a}^{b} f (x) d x = \int_{α}^{β} f (φ (t)) φ^{'} (t) d t

$x$ 积分的上，下限与 $t$ 积分的上下限由 $x = φ (t)$ 对应

Proof
$\begin{aligned} 设 F^{'} (x) = f (x), 则 \int_{a}^{b} f (x) d x = F (b) - F (a) \\ 而 \int f (φ (t)) φ^{'} (t) d t = \int f (φ (t)) d φ (t) = F (φ (t)) + C \\ 故 \int_{a}^{b} f (φ (t)) φ^{'} (t) d t = F [φ (t)] |_{a}^{b} = F (b) - F (a) \end{aligned}$

例题

Example

例题11 计算 $\int_{0}^{a} \sqrt{a^{2} - x^{2}} d x (a > 0)$

Solution

几何法

$S = \frac{π}{4} a^{2}$

代数法： #三角代换

$\begin{aligned} 令 x & = a \sin t \\ 原式 & = \int_{0}^{π / 2} \sqrt{a^{2} - a^{2} \sin^{2} t} \cdot a \cos t d t & 设为 \frac{p i}{2} 不用加绝对值 \\ = a^{2} \int_{0}^{π / 2} \cos^{2} t d t \\ = \frac{a^{2}}{2} \int_{0}^{π / 2} (1 + \cos 2 t) d t & 运用降幂公式 \\ = \frac{π}{4} a^{2} + a^{2} \frac{\sin 2 t}{4} |_{0}^{π / 2} \\ = \frac{π}{4} a^{2} \end{aligned}$

Example

设 $f$ 连续且 $f (x) = \sin 2 x + \int_{0}^{π / 2} f (x) d x$

Analysis

$f (x) = \sin 2 x + \underset{一个常数}{\underset{⏟}{\int_{0}^{π / 2} f (x) d x}}$

Solution
$\begin{aligned} 令 & \int_{0}^{π / 2} f (x) d x = A \\ 则 & f (x) = \sin 2 x + A \\ 两边积分: \\ \int_{0}^{π / 2} f (x) d x \\ = \int_{0}^{π / 2} \sin 2 x d x + (\frac{π}{2} - 0) A \\ A & = - \frac{1}{2} \cos 2 x |_{0}^{π / 2} + \frac{π}{2} A \\ = - \frac{1}{x} (- 1 - 1) + \frac{π}{2} A \\ ∴ A & = \frac{2}{2 - π} \\ 故 f (x) & = \sin 2 x + \frac{2}{2 - π} \end{aligned}$

关于原点对称的区间 / 奇/偶函数

Example

例13 设 $f \in C [- a, a]$ , 证明：

\int_{- a}^{a} f (x) d x = {\begin{cases} 0, & f (x) is odd \\ 2 \int_{0}^{s} f (x) d x, & f (x) is even \end{cases}

Proof
$\begin{aligned} \int_{- a}^{a} f (x) d x & = \int_{- a}^{0} f (x) d x + \int_{0}^{a} f (x) d x \\ \overset{x = - t}{=} \int_{a}^{0} f (- t) d (- t) + \int_{0}^{a} f (x) d x \\ = \int_{0}^{a} f (- t) d t + \int_{0}^{a} f (x) d x \\ = \int_{0}^{a} [f (- x) + f (x)] d x & 更换积分字母，积分值不变 \\ = \dots \end{aligned}$
Tips

该方法可以运用在关于原点对称的区间

周期函数定积分

$\int_{a}^{a + n T} f (x) d x = n \int_{0}^{T} f (x) d x$

Example

例 14 设 $f$ 是周期为 $T$ 的连续函数. 证明: $\forall a \in R$ , 有

\int_{a}^{a + T} f (x) d x = \int_{0}^{T} f (x) d x

Proof

$\int_{a}^{a + T} f (x) d x = (\int_{a}^{0} + \int_{0}^{T} + \int_{T}^{a + T}) f (x) d x$

下证: $\int_{a}^{0} 与 \int_{T}^{a + T}$ 抵消:

其中: $\int_{T}^{a + T} f (x) d x \overset{u = x - T}{=} \int_{0}^{a} f (u + T) d u$

$= \int_{0}^{a} f (u) d u \dots$ 周期性

代入得证

正余弦互换

在 $0 \sim \frac{π}{2}$ 对 $f (u, w)$ 积分

\int_{0}^{π / 2} f (\sin x, \cos x) d x = \int_{0}^{π / 2} f (\cos x, \sin x) d x

Example

例15 计算 $\int_{0}^{π / 2} \frac{\sin x}{\sin x + \cos x} d x$

Solution
$\begin{aligned} \int_{0}^{π / 2} \frac{\sin x}{\sin x + \cos x} d x & \overset{t = \frac{π}{2} - x}{=} \int_{π / 2}^{0} \frac{\sin (\frac{π}{2} - t)}{\sin (\frac{π}{2} - t) + \cos (\frac{π}{2} - t)} d t \\ = \int_{0}^{π / 2} \frac{\cos t}{\cos t + \sin t} d t \\ = \int_{0}^{π / 2} \frac{\cos x}{\sin x + \cos x} d x \end{aligned}$ $\begin{aligned} ⟹ \int_{0}^{π / 2} \frac{\sin x}{\sin x + \cos x} d x \\ = \frac{1}{2} (\int_{0}^{π / 2} \frac{\sin x}{\sin x + \cos x} + \int_{0}^{π / 2} \frac{\cos x}{\sin x + \cos x} d x) \\ = \frac{1}{2} \int_{0}^{π / 2} 1 d x \\ = \frac{π}{4} \end{aligned}$

分部积分法

#分部积分法

若 $u^{'} (x),$ $v^{'} (x) \in C [a, b]$ 则

\int_{a}^{b} u (x) v^{'} (x) d x = u (x) v (x) |_{a}^{b} - \int_{a}^{b} u^{'} (x) v (x) d x

例题

Example

$\int_{0}^{1 / 2} \arcsin x d x$

Solution
$\begin{aligned} 原式 & = x \arcsin x d x |_{0}^{1 / 2} - \int_{0}^{1 / 2} \frac{x}{\sqrt{1 - x^{2}}} d x \\ = \frac{1}{2} \cdot \frac{π}{6} - [- \frac{1}{2} \int_{0}^{1 / 2} \frac{d (1 - x^{2})}{\sqrt{1 - x^{2}}}] \\ = \frac{π}{12} + \sqrt{1 - x^{2}} |_{0}^{1 / 2} \\ = \frac{π}{12} + \frac{\sqrt{3}}{2} - 1 \end{aligned}$

Wallis 公式

#Wallis公式

$I n = \underset{三角函数互换}{\underset{⏟}{\int_{0}^{π / 2} \sin^{n} x d x = \int_{0}^{π / 2} \cos^{n} x d x}} = {\begin{cases} \frac{(n - 1)!!}{n!!} \cdot \frac{π}{2}, & n is even \\ \frac{(n - 1)!!}{n!!}, & n is odd \end{cases}$

Example

例16 证明 #Wallis公式

Proof
$\begin{aligned} I n & = - \int_{0}^{π / 2} \sin^{n - 1} x d \cos x \\ = - \sin^{n - 1} x \cos x |_{0}^{π / 2} + (n - 1) \int_{0}^{π / 2} \cos^{2} x \sin^{n - 2} x d x \\ = (n - 1) \int_{0}^{π / 2} \sin^{n - 2} x (1 - \sin^{2} x) d x \\ = (n - 1) (I_{n - 2} - I_{n}) \end{aligned}$ $\begin{aligned} ⟹ I n & = \frac{n - 1}{n} I_{n - 2}, 其中 I_{0} = \frac{π}{2}, I_{1} = \int_{0}^{π / 2} \sin x d x = 1 \\ ⟹ I n & = {\begin{cases} \frac{n - 1}{n} \cdot \frac{n - 3}{n - 2} \cdot \dots \cdot \frac{1}{2} I_{0} = \frac{(n - 1)!!}{n!!} \cdot \frac{π}{2}, & n is even \\ \frac{n - 1}{n} \cdot \frac{n - 3}{n - 2} \cdot \dots \cdot \frac{1}{2} I_{1} = \frac{(n - 1)!!}{n!!} \cdot 1, & n is odd \end{cases} \end{aligned}$
P.S. $!!$ - 双阶乘

Example

例17 计算

$I_{1} = \int_{0}^{2 π} \sin^{6} x d x$
$\int_{0}^{1} x^{2} \sqrt{s - x^{2}} d x$

1. Solution
$\begin{aligned} π 为周期 \\ ⟹ I_{1} = 2 \int_{0}^{π} \sin^{6} x d x \\ 关于 \frac{π}{2} 对称 \int_{0}^{π / 2} = \int_{\frac{π}{2}}^{π} \\ I_{1} = 4 \int_{0}^{π / 2} \sin^{6} x d x \end{aligned}$
根据 #Wallis公式

$I_{1} = 4 \frac{5!!}{6!!} \cdot \frac{π}{2}$

Addition

若改为 $\sin^{7} x$
$\begin{aligned} ∵ π 为周期 \\ ⟹ \int_{- π}^{π} 奇函数 d x = 0 \end{aligned}$

2.Solution
$\begin{aligned} I_{2} & \overset{x := \sin t}{=} \int_{0}^{π / 2} \sin^{2} \cos t d \sin t \\ = \int_{0}^{π / 2} (1 - \cos^{2} t) \cdot \cos^{2} t d t \\ = \int_{0}^{π / 2} \cos^{2} t d t + \int_{0}^{π / 2} \cos^{4} t d t \\ = (\frac{1!!}{2!!} - \frac{3!!}{4!!}) \cdot \frac{π}{2} \\ = \frac{π}{16} \end{aligned}$

七、积分余项 Taylor 公式

#积分余项Taylor公式

设 $f (x) \in C^{(n + 1)} U (a)$ 则 $\forall x \in U (a)$ , 有

\begin{aligned} f (x) & = \sum_{k = 0}^{n} \frac{f^{(k)} (a)}{k!} (x - a)^{k} + \frac{1}{n!} \int_{a}^{x} f^{(n + 1)} (t) (x - t)^{n} d t \\ \overset{def}{=} T_{n} + R_{n} \end{aligned}

分析：将余项 $R_{n} (a) = f - T_{n}$ 视为 $a$ 的函数写成积分形式

R_{n} (a) = - \int_{a}^{x} R_{n}^{'} (t) d t (R_{n} (x) = 0)

Proof
$\begin{aligned} f (x) & = f (a) + \int_{a}^{x} f^{'} (t) d t \\ = f (a) - \int_{a}^{x} f^{'} (t) d (x - t) \\ = f (a) - f (t) (x - t) |_{t = a}^{t = x} + \int_{a}^{x} (x - t) f^{″} (t) d t \\ = f (a) + f^{'} (a) (x - a) - \frac{1}{2!} \int_{a}^{x} f^{″} (t) d (x - t)^{2} \\ = f (a) + f^{'} (a) (x - a) - \frac{1}{2!} f^{″} (t) (x - t) |_{t = a}^{t = x} + \frac{1}{2!} \int_{a}^{x} (x - t)^{2} f^{‴} (t) d t \\ = f (a) + f^{'} (a) (x - a) + \frac{f^{″} (a)}{2!} (x - a) + \dots \\ 以此类推... \end{aligned}$

Lagrange 余项 Taylor 公式

Formula

$R_{n} = \frac{f^{(n + 1)} (ξ)}{n!} \int_{a}^{x} (x - t)^{n} d t = \frac{f^{(n + 1)} (ξ)}{(n + 1)!} (x - a)^{n + 1}$

Homework

设函数 $f (x)$ 在 $[a, b]$ 上连续，而 $g (x)$ 在 $[a, b]$ 上可积且是非负的（或非正的），证明：

存在 $ξ \in [a, b]$ ，使得

\int_{a}^{b} f (x) g (x) d x = f (ξ) \int_{a}^{b} g (x) d x

Tips 与积分中值定理类似地证明

Cauchy 余项的 Taylor 公式

Formula

$\begin{aligned} R_{n} & = \frac{f^{n + 1} (ξ)}{n!} (x - ξ)^{n} (x - a) \\ = \frac{f^{n + 1} (a + θ h)}{n!} (1 - θ)^{n} h^{n + 1} \\ 其中 θ = a + θ (x - a) \overset{def}{=} a + θ h \end{aligned}$

$x - ξ = (x - a) - θ h = (1 - θ) h$

一、定积分的定义

曲边梯形面积

变速直线运动位移

定积分

Riemann和或积分和

f∈R[a,b] 的含义?

可积与不可积的 “ε−δ” 表述 ?

例题

二、可积函数类

常见的可积条件==（闭区间）==

例题

三、积分例子初识

例题

四、积分的基本性质

可加性

※子区间可积

线性性

※改变有限点不改变可积性与积分值

保号性

单调性

估值性

※积分绝对值不超过绝对值的积分

🔴积分中值定理

五、微积分基本定理

变上限积分

连续性

可导性

例题

变上限积分求导

变上限积分求极限

借助 #积分/中值定理 求变上限积分的极限

原函数存在定理

微积分基本定理

🔴弱形式 N-L公式

六、定积分的计算

换元积分法

例题

关于原点对称的区间 / 奇/偶函数

周期函数定积分

正余弦互换

分部积分法

例题

Wallis 公式

七、积分余项 Taylor 公式

Lagrange 余项 Taylor 公式

Cauchy 余项的 Taylor 公式

$f \in R [a, b]$ 的含义?

可积与不可积的 “ $ε - δ$ ” 表述 ?

借助 #积分/中值定理求变上限积分的极限